Trong các bài toán toán học, việc tìm ước chung lớn nhất (UCLN) của hai số là một bước quan trọng giúp giải quyết nhiều bài toán khác nhau. Tuy nhiên, với sự phát triển của công nghệ, chúng ta có thể tìm UCLN của hai số trên máy tính một cách nhanh chóng và chính xác. Trong bài viết này, techmienphi.com sẽ hướng dẫn chi tiết nhất về cách tìm UCLN trên máy tính.
UCLN trên máy tính là gì
Mục Lục
UCLN (ước chung lớn nhất) trên máy tính là một phép tính toán để tìm ra ước chung lớn nhất của hai hoặc nhiều số nguyên dương. Đây là một trong những khái niệm cơ bản trong toán học và được sử dụng rộng rãi trong nhiều lĩnh vực khác nhau, như trong thuật toán mã hóa, thiết kế mạch điện tử, kỹ thuật số, v.v.
Việc tìm UCLN giúp cho chúng ta có thể đưa các số nguyên về dạng tối giản và chia các số nguyên đó cho UCLN sẽ giúp ta thu được kết quả phép chia tối giản.

Hướng dẫn cách tìm ucln trên máy tính chi tiết
Phương pháp Euclid tìm UCLN trên máy tính
Phương pháp Euclid là một phương pháp đơn giản và hiệu quả để tìm UCLN của hai hoặc nhiều số nguyên dương. Đây cũng là phương pháp tìm UCLN phổ biến nhất và được sử dụng rộng rãi trên máy tính.
Các bước để sử dụng phương pháp Euclid để tìm UCLN như sau:
Bước 1: Nhập vào hai hoặc nhiều số nguyên dương cần tìm UCLN.
Bước 2: Sử dụng phương pháp Euclid để tìm UCLN. Phương pháp Euclid là tìm ước chung lớn nhất bằng cách thực hiện phép chia chia đôi lặp lại cho đến khi số dư bằng 0. Cụ thể, ta thực hiện các bước sau:
- Lấy số lớn hơn trong hai số ban đầu làm số chia, số nhỏ hơn làm số bị chia.
- Thực hiện phép chia: chia số chia cho số bị chia và lấy phần dư.
- Nếu phần dư bằng 0, số bị chia là UCLN.
- Nếu phần dư khác 0, ta lấy phần dư làm số chia và lặp lại từ bước 2.
Bước 3: Xuất kết quả UCLN.
Ví dụ: Tìm UCLN của 24 và 36 bằng phương pháp Euclid
Bước 1: Nhập vào 24 và 36.
Bước 2: Áp dụng phương pháp Euclid:
- Chọn 36 làm số chia và 24 làm số bị chia.
- 36 chia cho 24, ta được 1 dư 12.
- Lấy 12 làm số chia và 24 làm số bị chia.
- 24 chia cho 12, ta được 2 dư 0.
- Vậy UCLN của 24 và 36 là 12.
Bước 3: Xuất kết quả UCLN là 12.
Chúng ta có thể sử dụng phương pháp Euclid để tìm UCLN của bất kỳ hai hoặc nhiều số nguyên dương nào trên máy tính.
Tìm UCLN trên máy tính bằng lập trình
Để tìm UCLN của hai số trên máy tính bằng lập trình, chúng ta có thể sử dụng thuật toán Euclid. Thuật toán này được xây dựng dựa trên việc lấy số lớn chia cho số bé, sau đó lấy số bé chia cho số dư của phép chia trước đó và tiếp tục như vậy cho đến khi số dư bằng 0. Lúc đó, số chia là UCLN của hai số ban đầu.
Dưới đây là ví dụ về cách tìm UCLN của hai số bằng lập trình bằng ngôn ngữ Python:
def gcd(a, b):
if b == 0:
return a
else:
return gcd(b, a % b)
a = int(input(“Nhập số thứ nhất: “))
b = int(input(“Nhập số thứ hai: “))
print(“UCLN của”, a, “và”, b, “là”, gcd(a, b))
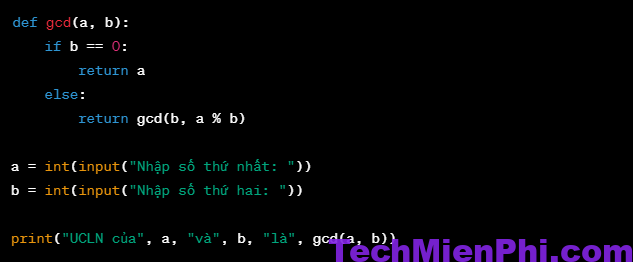
Trong đoạn code trên, hàm gcd(a, b) sử dụng đệ quy để tính UCLN của hai số a và b. Lưu ý rằng nếu số b bằng 0, thì hàm sẽ trả về số a. Trong phần còn lại của chương trình, chúng ta sử dụng hàm input() để nhận đầu vào từ người dùng và sử dụng hàm print() để hiển thị kết quả.
Ngoài ra, các ngôn ngữ lập trình khác như C++, Java, C# cũng cung cấp các thuật toán để tính UCLN. Bạn có thể tìm hiểu thêm về cách tìm UCLN trên máy tính bằng lập trình bằng các ngôn ngữ này.
Cách tính UCLN trên máy tính casio
Dưới đây là các bước chi tiết để tính UCLN trên máy tính Casio:
Bước 1: Bật máy tính Casio
Bước 2: Nhập hai số nguyên dương cần tính UCLN, ví dụ 36 và 48.
Bước 3: Chọn chế độ “GCD” hoặc “HCF” trên máy tính Casio. Thông thường, chế độ này được đánh dấu trên nút “GCD” hoặc “HCF”.
Bước 4: Nhấn nút “=” để hiển thị kết quả UCLN của hai số. Trong ví dụ này, kết quả UCLN là 12.
Lưu ý: Trong một số dòng máy tính Casio, chế độ UCLN có thể được đặt tên khác nhau. Nếu bạn không thể tìm thấy chế độ GCD hoặc HCF trên máy tính của mình, hãy tham khảo tài liệu hướng dẫn sử dụng của máy tính để tìm cách thực hiện tính toán này trên máy tính của bạn,
Sử dụng phần mềm tính toán tìm UCLN
Bạn có thể sử dụng các phần mềm tính toán như Microsoft Excel, MATLAB, hoặc Wolfram Alpha để tìm UCLN của hai số.
Ví dụ, để tính UCLN của hai số a và b bằng Microsoft Excel, bạn có thể sử dụng công thức sau:
= GCD(a, b)
Trong đó, “GCD” là viết tắt của “Greatest Common Divisor” (UCLN).
Ví dụ, để tính UCLN của hai số 15 và 25 trong Excel, bạn có thể nhập công thức sau vào một ô trống:
= GCD(15, 25)
Sau đó, nhấn Enter, và kết quả UCLN của hai số sẽ được hiển thị.
Tương tự, để tính UCLN của hai số a và b trong MATLAB, bạn có thể sử dụng lệnh sau:
gcd(a, b)
Nếu bạn sử dụng Wolfram Alpha, bạn có thể nhập các số của bạn vào trang web và nhập “gcd(a,b)” vào công cụ tính toán của trang web để tìm UCLN.
Lưu ý rằng nếu bạn đang sử dụng một phần mềm hoặc công cụ trực tuyến khác, cú pháp hoặc cách sử dụng có thể khác nhau.
Thuật toán tìm UCLN trên máy tính
Thuật toán tìm UCLN trên máy tính được gọi là thuật toán Euclid. Có hai phiên bản của thuật toán này: Euclid cổ điển và Euclid mở rộng. Dưới đây là thuật toán Euclid cổ điển:
- Nhập vào hai số nguyên a và b.
- Nếu b = 0 thì trả về giá trị của a.
- Ngược lại, thực hiện phép chia lấy dư a/b và gán kết quả cho r.
- Gán a=b và b=r.
- Quay lại bước 2.
Thuật toán Euclid mở rộng cũng dựa trên thuật toán Euclid cổ điển, tuy nhiên nó cho phép tính cả hai hệ số tương ứng với a và b. Hệ số tương ứng với a được gọi là x và hệ số tương ứng với b được gọi là y. Thuật toán Euclid mở rộng được sử dụng để giải các bài toán liên quan đến việc tìm một số nguyên x, y sao cho ax + by = gcd(a, b).
Dưới đây là pseudocode của thuật toán Euclid cổ điển:
function Euclid(a, b)
while b ≠ 0 do
r ← a mod b
a ← b
b ← r
end while
return a
end function
Và đây là pseudocode của thuật toán Euclid mở rộng:
function ExtendedEuclid(a, b)
if b = 0 then
return (a, 1, 0)
else
(d, x', y') ← ExtendedEuclid(b, a mod b)
x ← y'
y ← x' - ⌊a/b⌋ * y'
return (d, x, y)
end if
end function
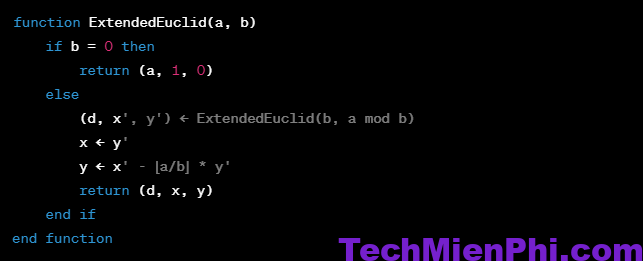
Trong đó, d là UCLN của a và b, x và y là các hệ số tương ứng với a và b.
Bước sóng Euclid tìm UCLN trên máy tính
“Bước sóng Euclid” (Euclidean algorithm) là một thuật toán tìm ước chung lớn nhất (UCLN) của hai số nguyên dương a và b. Thuật toán được đặt theo tên của nhà toán học Euclid, người đầu tiên phát triển phương pháp này.
Các bước để tìm UCLN bằng thuật toán Euclid như sau:
- Nhập vào hai số nguyên dương a và b.
- Thực hiện phép chia lấy dư a/b và gán kết quả cho r.
- Nếu r = 0 thì trả về giá trị của b là UCLN của a và b.
- Ngược lại, gán a=b và b=r và quay lại bước 2.
Các bước này được lặp lại cho đến khi r = 0, khi đó giá trị của b sẽ là UCLN của a và b.
Ví dụ, để tìm UCLN của 40 và 24, ta thực hiện các bước sau:
- a = 40, b = 24
- a/b = 1 dư 16, r = 16
- a = 24, b = 16
- a/b = 1 dư 8, r = 8
- a = 16, b = 8
- a/b = 2 dư 0, r = 0
- UCLN của 40 và 24 là 8.
Thuật toán Euclid còn có thể được mở rộng để tính toán các hệ số tương ứng với a và b trong phương trình ax + by = gcd(a, b).
Cách tìm ucln và bcnn trên máy tính casio 580
Để tìm UCLN và BCNN của hai số trên máy tính Casio 580, bạn có thể làm theo các bước sau:
- Nhập hai số cần tính UCLN và BCNN vào máy tính bằng cách ấn các nút tương ứng trên bàn phím.
- Chọn chế độ tính toán UCLN bằng cách ấn phím SHIFT, sau đó phím SIN (GCD).
- Màn hình hiển thị UCLN của hai số bạn đã nhập vào.
- Để tính BCNN, chọn chế độ tính toán BCNN bằng cách ấn phím SHIFT, sau đó phím COS (LCM).
- Màn hình hiển thị BCNN của hai số bạn đã nhập vào.
Lưu ý rằng trên một số phiên bản của máy tính Casio 580, chế độ tính toán UCLN và BCNN có thể khác nhau. Bạn có thể kiểm tra hướng dẫn sử dụng của máy tính để biết thêm thông tin chi tiết về cách tính UCLN và BCNN.
Cách tìm ucln và bcnn trên máy tính casio 570es
Để tìm UCLN và BCNN của hai số trên máy tính Casio fx-570ES, bạn có thể làm theo các bước sau:
- Bật máy tính và đảm bảo rằng chế độ toán học được chọn bằng cách nhấn phím “MODE” và chọn “2: MATH” (hoặc “2: MTH” trên một số phiên bản khác).
- Nhập hai số cần tìm UCLN và BCNN.
- Nhấn phím “SHIFT” và sau đó là phím “DRG” để mở menu chức năng.
- Sử dụng phím mũi tên để di chuyển đến “FRAC”, sau đó nhấn “=”. Màn hình sẽ hiển thị các số ở dạng phân số.
- Nhấn phím “OPTN” và sau đó là phím “F4” để mở menu chức năng.
- Sử dụng các phím mũi tên để di chuyển đến “GCD” (tức UCLN) hoặc “LCM” (tức BCNN), sau đó nhấn “=”.
- Màn hình sẽ hiển thị kết quả của UCLN hoặc BCNN của hai số đã nhập.
Lưu ý: Nếu bạn muốn tính UCLN và BCNN của nhiều số hơn hai, bạn có thể nhập chúng vào máy tính và sử dụng chức năng tương tự để tìm kết quả.
Tìm ước chung lớn nhất trong java
Để tìm ước chung lớn nhất của hai số trong Java, bạn có thể sử dụng thuật toán Euclid. Dưới đây là một ví dụ về cách tìm UCLN của hai số nguyên a và b trong Java
public class Main {
public static void main(String[] args) {
int a = 40;
int b = 24;
int ucln = findGCD(a, b);
System.out.println(“UCLN của ” + a + ” và ” + b + ” là: ” + ucln);
}
public static int findGCD(int a, int b) {
while (b != 0) {
int r = a % b;
a = b;
b = r;
}
return a;
}}
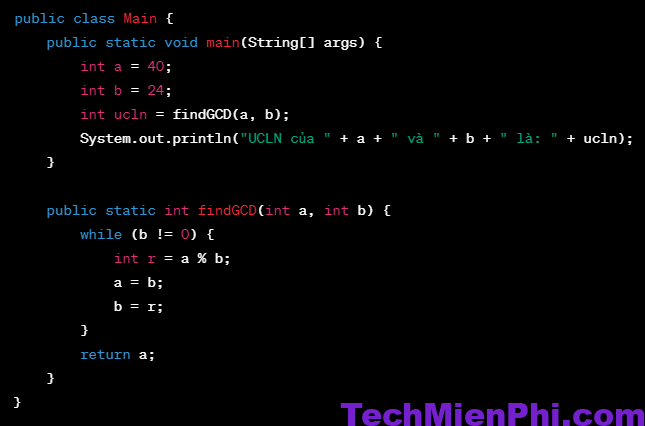
Kết quả đầu ra của chương trình này sẽ là:
UCLN của 40 và 24 là: 8
Trong đó, phương thức findGCD thực hiện thuật toán Euclid để tìm UCLN của hai số nguyên a và b. Trong mỗi vòng lặp, phương thức này tính toán phép chia lấy dư của a/b và gán kết quả cho biến r. Sau đó, a được gán b và b được gán r. Việc lặp lại quá trình này cho đến khi r = 0 sẽ cho chúng ta giá trị UCLN của a và b.
Tìm ước chung lớn nhất bằng c++
Để tìm ước chung lớn nhất (UCLN) của hai số a và b trong C++, bạn có thể sử dụng thuật toán Euclid như sau:
#include <iostream>
using namespace std;
int main() {
int a, b;
cout << “Nhap hai so a va b: “; cin >> a >> b;
// tìm ước chung lớn nhất bằng thuật toán Euclid
while (b != 0) {
int r = a % b;
a = b;
b = r;
}
cout << “Uoc chung lon nhat cua a va b la: ” << a << endl;
return 0;
}
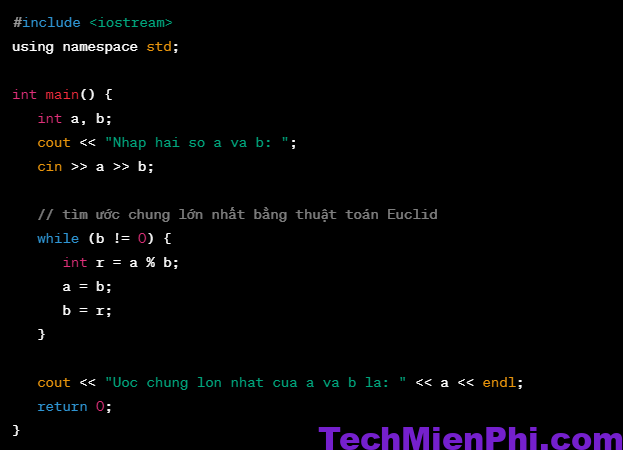
Trong đó, biến a và b lần lượt lưu giá trị của hai số cần tìm UCLN. Vòng lặp while sử dụng thuật toán Euclid để tìm UCLN của hai số đó. Cuối cùng, kết quả được hiển thị trên màn hình.
Kết Luận
Trên đây là hướng dẫn chi tiết về cách tìm ước chung lớn nhất (UCLN) của hai số nguyên dương trên máy tính, bao gồm cách sử dụng thuật toán Euclid để giải quyết bài toán này. Việc tìm UCLN là một thủ tục quan trọng trong toán học và có nhiều ứng dụng trong thực tế. Hy vọng rằng hướng dẫn này sẽ giúp bạn có thể áp dụng thuật toán Euclid để tìm UCLN một cách dễ dàng trên máy tính.